Total Internal Reflection

Total internal reflection (TIR) is the phenomenon that involves the reflection of all the incident light off the boundary. TIR only takes place when both of the following two conditions are met:

• a light ray is in the more dense medium and approaching the less dense medium.
• the angle of incidence for the light ray is greater than the so-called critical angle.

In our introduction to TIR, we used the example of light traveling through water towards the boundary with a less dense material such as air. When the angle of incidence in water reaches a certain critical value, the refracted ray lies along the boundary, having an angle of refraction of 90-degrees. This angle of incidence is known as the critical angle; it is the largest angle of incidence for which refraction can still occur. For any angle of incidence greater than the critical angle, light will undergo total internal reflection.

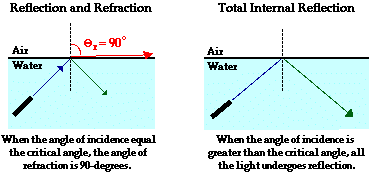
So the critical angle is defined as the angle of incidence that provides an angle of refraction of 90-degrees. Make particular note that the critical angle is an angle of incidence value. For the water-air boundary, the critical angle is 48.6-degrees. For the crown glass-water boundary, the critical angle is 61.0-degrees. The actual value of the critical angle is dependent upon the combination of materials present on each side of the boundary.

Let's consider two different media - creatively named medium i (incident medium) and medium r (refractive medium). The critical angle is the that gives a value of 90-degrees. If this information is substituted into Snell's Law equation, a generic equation for predicting the critical angle can be derived. The derivation is shown below.

n_i *• sine() = n_r • sine ()

n_i • sine() = n_r • sine (90 degrees)

n_i • sine() = n_r

sine() = n_r/n_i

= sine^-1 (n_r/n_i) = invsine (n_r/n_i)

The critical angle can be calculated by taking the inverse-sine of the ratio of the indices of refraction. The ratio of n_r/n_i is a value less than 1.0. In fact, for the equation to even give a correct answer, the ratio of n_r/n_i must be less than 1.0. Since TIR only occurs if the refractive medium is less dense than the incident medium, the value of n_i must be greater than the value of n_r. If at any time the values for the numerator and denominator become accidentally switched, the critical angle value cannot be calculated. Mathematically, this would involve finding the inverse-sine of a number greater than 1.00 - which is not possible. Physically, this would involve finding the critical angle for a situation in which the light is traveling from the less dense medium into the more dense medium - which again, is not possible.

This equation for the critical angle can be used to predict the critical angle for any boundary, provided that the indices of refraction of the two materials on each side of the boundary are known. Examples of its use are shown below:

Example A Calculate the critical angle for the crown glass-air boundary. Refer to the table of indices of refraction if necessary.

The solution to the problem involves the use of the above equation for the critical angle.

= sin^-1 (n_r/n_i) = invsine (n_r/n_i)

= sin^-1 (1.000/1.52) = 41.1 degrees

Example B Calculate the critical angle for the diamond-air boundary. Refer to the table of indices of refraction if necessary.

The solution to the problem involves the use of the above equation for the critical angle.

= sin^-1 (n_r/n_i) = invsine (n_r/n_i)

= sin^-1 (1.000/2.42) = 24.4 degrees

TIR and the Sparkle of Diamonds

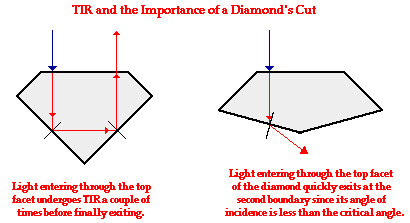
Relatively speaking, the critical angle for the diamond-air boundary is an extremely small number. Of all the possible combinations of materials that could interface to form a boundary, the combination of diamond and air provides one of the largest differences in the index of refraction values. This means that there will be a very small n_r/n_i ratio and subsequently a small critical angle. This peculiarity about the diamond-air boundary plays an important role in the brilliance of a diamond gemstone. Having a small critical angle, light has the tendency to become "trapped" inside of a diamond once it enters. A light ray will typically undergo TIR several times before finally refracting out of the diamond. Because the diamond-air boundary has such a small critical angle (due to diamond's large index of refraction), most rays approach the diamond at angles of incidence greater than the critical angle. This gives diamond a tendency to sparkle. The effect can be enhanced by the cutting of a diamond gemstone with a strategically planned shape. The diagram below depicts the total internal reflection within a diamond gemstone with a strategic and a non-strategic cut.

Share :

Tweet

More

Related Post